Math of Tangents
The faint blue line meandered through the city streets, thousands of weary marathon runners following it as their guide through the 26.2 mile circuit. The wall of runners approached yet another bend in the road. Without thinking, some of the athletes taking the outside line put themselves at a disadvantage by running further. While one corner won’t make much difference in a marathon, over a common race course with turns, taking the outside line can make quite a difference. How much of a difference? After so many years on the race course, I continue to be amazed by the number of athletes who appear to run with no concern whatsoever for the specific path they follow. This article outlines some concepts that may be very intuitive to racers, yet once on the race course, it is often the case that these ideas are ignored.
The Math
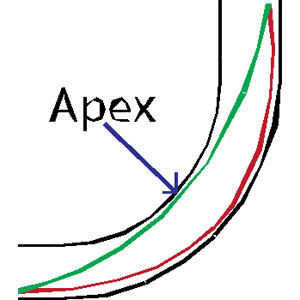
The shortest distance between two points is a straight line. On a straight road, running anything other than a straight line will result in running further, and all things being equal, a slower run time. Adding a curve to a path allows a choice of routes through the curve: From following the curb on the inside track, cutting a tangent, or following the outside curb, each route can either be shorter or longer. A tangent is defined as a straight line that touches a curved line at only one point (see Figure 1, green line). The apex of a turn is generally the geometric center of the turn; the tightest part of a corner. Consider the following example on a route with a single quarter turn, and a route starting and ending at the same point:
As you can see in Figure 1, the shortest distance between two points is as straight a line as possible within the confines of a race course, as indicated by the green line. The red route follows the outside of the curve and necessitates a longer distance. You're probably thinking "I know that! It's obvious!" and indeed it is. Keep your eyes open at your next race and notice how many runners take the longer route: you'll be amazed. Just don't be one of them.
The situation gets slightly more complicated when you add two or more turns of different directions. While the shortest distance around each turn is the inside line, the interface between the two turns necessitates approaching the second turn from the first, offering the choice for any number of paths. In this instance, looking ahead and sighting for the apex of the second turn will minimize the distance traveled.

How does this affect the distance run over the course of a real-life course? I measured a 2.54 km route on the road using a calibrated cycle computer, as measured by taking the inside line and apex of every curve when possible and legal, trying to minimize the distance while staying within my lane. My course consisted of some neighborhood streets with 6 right angle turns and one long sweeping curve. I then measured the same route, this time taking the outside or likely the longest distance while staying within my lane. What did I find? On a decidedly average course with 6 turns, the longer route measured 2.60 km, 2.4 % further than the shortest distance possible. For a 20 minute 5K effort, this extra 2.4 % translates to an added distance of 120 meters that is equal to an added 29 seconds to the base time- for no reason other than the choice of routing. By the same token, imagine an improvement of 29 seconds on a 5K simply by choosing the shortest and most direct route. While this is only an example and each course will allow for different savings based on route choice, all other things being equal (route conditions, runner congestion, etc…) an athlete will lose time by running further then necessary.
In a cycling race, a similar theory applies, with the caveat that bikes don’t corner like runners due to higher speeds and the need to maintain balance and traction. Also, cycling an additional 2-3% distance at higher speeds means a smaller time gap than in running. Cyclists who generally keep to the apex of the turns are going to ride a shorter distance than other paths. Provided an athlete follows the race rules, cutting the tangent is legal and worth some free time. Properly marked courses are measured at their shortest distance. Why go further?
Real-life suggestions
– Be course-aware. Explore the race route before race day and note where the shortest route may be, upcoming corners on the far side of blind hills, road conditions, etc…
– During the run, consider that you'll likely be moving from one side of the road to the other, sometimes to the confusion of those around you. Don't get in their way or cause a situation that is hazardous. Many runners really do run the red route in Figure 2 above…if you are taking the green route, keep your eyes open and be ready to hop aside as needed. Most runners don't run the shortest route.
– Keep your head up! Look ahead on the course at all times and make continual judgments to run the most direct and straightest course possible. Once at the apex of one curve, sight for the apex of the next curve, or if you can see further ahead, sight directly for the apex of the curve furthest away. Run a straight line between the apex of each curve.
– Trail or pavement quality is often less ideal at the edges of the course. Watch for curbs, potholes and poison oak, taking reasonable care to balance running speed and safety with running the shortest course. Sometimes it is okay to run a little further to the finish line.
Clearly there are other real-life conditions at play here, including the need to avoid obstacles (mud, potholes), people, traffic and to benefit from aid stations. Once again, most athletes conceptually understand the idea of a shortest route, but do not execute on that plan whilst racing. However, with the effort with which we approach our training to cut off a couple of percent of our race time, choosing the right path may be worth as much as the best coaching in the world. So keep your coach, but also consider your race routing. Next time you see somebody struggling on a race course, instead of shouting “you’re nearly there”, perhaps some more helpful advice would be “remember to cut the tangents”.
Jonathan Toker, in addition to acting as the Slowtwitch Science Editor, is an elite-level triathlete/trail runner who hails from Canada and lives in Southern California. He received a Ph.D. in organic chemistry from The Scripps Research Institute in 2001 and worked at biotech Amgen for four years. Jonathan invented the SaltStick products back in 2002, available online as well as at better retailers.